Drehimpuls

• Sie kennen den Drehimpuls und die Ursache für eine Drehimpulsänderung
• Sie können qualitativ Erscheinung, die mit dem Drehimpuls zusammenhängen erklären

Jeder um eine feste Achse rotierende Körper besitzt einen Drehimpuls. Ähnlich dem Impuls bleibt er in einem abgeschlossenen System erhalten (Drehimpulserhaltung). Für den Drehimpuls eines Körpers mit dem Trägheitsmoment $J$, der um eine feste Achse mit der Winkelgeschwindigkeit $\omega$ rotiert, gilt:

$$\vec{L}=J\vec{\omega}$$

Um den Drehimpuls eines Körpers zu ändern braucht es ein Drehmoment $M$ und Zeit $\Delta t$:

$$\Delta\vec{L}=\vec{M}\Delta t$$

Es ist immer wieder erstaunlich, wie Eiskunstläuferinnen und Eiskunstläufer auf dem Eis die wildesten Pirouetten zeigen können. Wer sich das einmal genauer zu Gemüte führen will, soll sich folgendes Video anschauen.

Für die ganz Schlauen: Im Kommentar hat sich ein Fehler eingeschlichen. Finden Sie ihn?

Wird an einem Velokreisel eine Masse angehängt, kippt das Rad nicht wesentlich in Richtung der angehängten Masse (wie Sie vermutlich erwarten würden), sondern beginnt seitlich um den Aufhängepunkt zu drehen. Man nennt diese seitliche Drehbewegung Präzession. Schauen Sie sich dazu das Video der ETH an:

Im Video wird auch die Nutation erwähnt. Diese brauchen Sie nicht zu kennen.

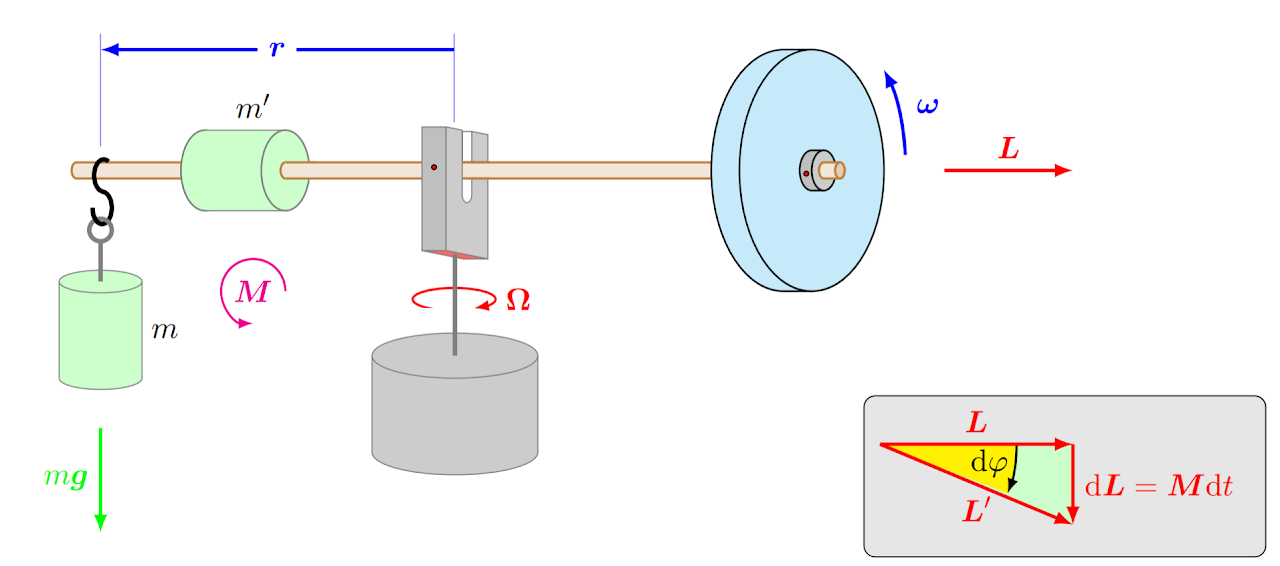
Wir möchten aber die Präzession verstehen. Sie hängt mit der Drehimpulsänderung zusammen. Unten ist der experimentelle Aufbau skizziert:

Die Masse $m'$ an der Achse sorgt dafür, dass das System bestehend aus blauem Rad, brauner Achse und grüner Masse $m'$ bezüglich der Drehachse DA in der Mitte (roter Punkt im grauen Gebilde) im Gleichgewicht ist. Das ist die Anfangssituation im Video oben. Dann wird das blaue Rad in Rotation versetzt. Mit der Rechte-Hand-Regel können Sie die Richtung des Winkelgeschwindigkeitsvektors bestimmen. Er zeigt nach rechts. Da der Drehimpuls die gleiche Richtung hat wie die Winkelgeschwindigkeit, zeigt auch er nach rechts (roter Pfeil in der Skizze). In dieser Situation wird eine Masse $m$ an einem Haken angehängt. Diese Masse bewirkt ein Drehmoment $M$ bezüglich der Drehachse DA (ist als violetter Pfeil in die Skizze gezeichnet). Wird dieses Drehmoment als Vektor dargestellt, greift dieser an der Drehachse an und zeigt nach vorne (Rechte-Hand-Regel). Dieses Drehmoment bewirkt laut der Grundgleichung für die Dynamik der Rotation eine Drehimpulsänderung:

$$\Delta\vec{L}=\vec{M}\Delta t$$

In der Skizze unten rechts ist diese Änderung eingezeichnet (für uns gilt $d = \Delta$; wir schauen uns kleine Differenzen und nicht infinitesimal kleine Änderungen an). Der Additionsplan zeigt die Situation von oben. Das Drehmoment bewirkt also, dass das Rad nicht nach links kippt, sondern sich seitlich im Uhrzeigersinn dreht.