Chaotisches Drehpendel

Lernziele

Sie untersuchen das chaotische Verhalten eines Drehpendels und lernen dabei unterschiedliche Darstellungsmethoden kennen, die einem helfen können, chaotisches Verhalten zu verstehen.
Sie kennen die Darstellungen des Phasenraumes und wissen, was eine Trajektorie ist.
Der Begriff Phasenverdoppelung ist Ihnen bekannt.

Der Versuchsaufbau

Nebenan ist ein chaotisches Drehpendel (auch Pohlsches Rad genannt) dargestellt. Der kupferfarbige Ring ist drehbar gelagert und mit der Spiralfeder verbunden. Ohne Reibung würde der Ring eine Drehschwingung ausführen (also wie ein Federpendel harmonisch schwingen). Um die Reibung zu kompensieren wird der Ring periodisch angeregt. Eine Wirbelstrombremse bremst die Schwingung und verhindert so die Resonanzkatastrophe. Die Wirkung der Wirbelstrombremse wird kontrolliert und heisst Dämpfung. Bei grosser Dämpfung wird die Bewegung des Rings stark eingeschränkt. Bei kleiner Dämpfung kann er sich stärker bewegen.

Zusätzlich wird eine kleine Masse am Ring angebracht (Unwucht). Diese Masse erzeugt eine nichtlineare Komponente und führt zu chaotischem Verhalten.

Beobachtung

Im folgenden Video sehen Sie, wie sich das Drehpendel unter verschiedenen Bedingungen verhält. Uns interessiert der 2. Teil des Films, wo die Dämpfung verkleinert wird. Bei grosser Dämpfung ungefähr in der Mitte des Videos, führt das Drehpendel eine voraussagbare Bewegung aus. Je kleiner die Dämpfung wird, desto chaotischer verhält sich die Bewegung. Im Diagramm nebenan wird teilweise die Winkelgeschwindigkeit in Abhängigkeit von der Position des Pendels (Winkel) dargestellt. Man nennt diese Darstellung den Phasenraum. Je regelmässiger die Bewegung, desto geordneter sieht der Phasenraum aus. Ist die Kurve in sich geschlossen, wiederholt sich die Bewegung periodisch und ist in einem gewissen Sinne voraussagbar. Ist die Kurve offen, deutet dies auf ein chaotisches Verhalten hin. Im Übrigen wird die dargestellte Kurve im Phasenraum Trajektorie genannt. Manchmal weist das Diagramm nebenan die Position / den Winkel gegenüber der Zeit auf. Das ist ein Elongation-Zeit-Diagramm, das wir von der Schwingung her bereits kennen.

Simulation

Die Bewegung des Drehpendels folgt einfachen, physikalischen Gesetzen. Sie wissen bereits von der Rotation her, dass für ein Drehpendel mit dem Trägheitsmoment $J$ gilt:

$$M_{\text{res}}=J\alpha$$

Das resultierende Drehmoment setzt sich aus folgenden Anteilen zusammen:

Spiralfeder der Härte $D$
Wirbelstrombremse mit der Dämpfung $\delta$
Periodische Anregung der Eigenfrequenz $f$
und der Zusatzmasse $m$ im Abstand $l$ von der Drehachse

Für das resultierende Drehmoment findet man folgenden Ausdruck (Sie brauchen ihn sich nicht zu merken!):

$$M_{\text{res}}=-D\varphi-\delta\omega+M_0\sin(2\pi ft)%2bmgl\sin\varphi$$

Sind am Anfang die Startbedingungen bekannt (Startwinkel $\varphi$ und Startgeschwindigkeit $\omega$), lässt sich damit die Winkelbeschleunigung $\alpha$ berechnen. Dann findet man für die neue Winkelgeschwindigkeit:

$$\omega_{\text{neu}}=\omega+\alpha\Delta t$$

Und für den neuen Winkel:

$$\varphi_{\text{neu}}=\varphi+\omega_{\text{neu}}\Delta t$$

Und das ganze Spiel beginnt mit dem neuen Winkel und der neuen Winkelgeschwindigkeit von vorne, indem man die neue Winkelbeschleunigung mit der langen Formel berechnet, etc.

Für die Zeitspannen $\Delta t$ werden sehr kurze Zeitabschnitte gewählt. So lässt sich die Entwicklung des Drehpendels mit der Zeit simulieren.

Aufgabe

Ich habe für Sie eine Tabellenkalkulation (Google Tabelle) vorbereitet. Sie können diese kopieren und anschliessend damit arbeiten. Sie können sie auch im Excelformat herunter laden und mit Ihrer Desktop-App arbeiten.

Hier eine Vorschau, die sich nicht bearbeiten lässt:

Bei den Starteinstellungen ist die Dämpfungszahl im Feld C6 noch null. Ändern Sie diesen Wert auf 0.0004. Was beobachten Sie im Elongations-Zeit-Diagramm (oben) und im Phasenraum (unten)?
«Schalten» Sie nun in der Simulation die äussere Anregung an, indem Sie im Feld C9 den Wert von 0 auf 0.01 ändern. Schrauben Sie auch die Dämpfzahl hoch auf 0.004. Das Pendel schwingt wieder harmonisch. So lässt sich die Reibung des Drehpendels in Wirklichkeit kompensieren.
Jetzt «bringen» Sie die Zusatzmasse an, indem Sie ins Feld C7 0.01 statt 0 hineinschreiben. Was beobachten Sie? Das Pendel schwingt nicht mehr symmetrisch um die Gleichgewichtslage, sondern nur noch auf der einen Seite. Der Phasenraum sieht wie ein Ei aus…
Spielen Sie ab jetzt nur noch mit der Dämpfungszahl im Feld C6. Wenn Sie diese sukzessive verkleinern, werden Sie mehr und mehr chaotische Bewegungen des Drehpendels beobachten. Versuchen Sie die Dämpfungszahl für die sog. Phasenverdoppelung zu finden. Dort werden wie zwei ineinander, greifende «Eier» beobachtet. Schaffen Sie es auch, eine Phasenvervierfachung zu beobachten? Seien Sie hartnäckig! Sie schaffen es schon.
Ab welcher Dämpfungszahl bildet die Trajektorie eine nicht mehr geschlossene Kurve? Unter dieser Dämpfzahl verhält sich das System chaotisch.
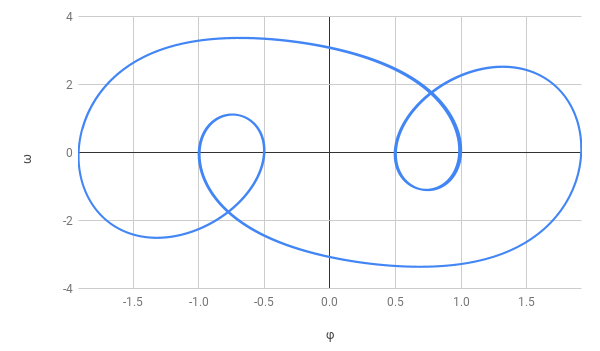
Suchen Sie nach «schönen» Trajektorien im Phasenraum. Ich selbst habe folgende gefunden.

Zusammenfassung

Das Drehpendel ist ein Beispiel, das deutlich macht, dass chaotische Systeme sich nicht immer chaotisch verhalten müssen. Sie können sehr wohl in einem gewissen Bereich ein vorhersehbares Verhalten aufweisen. Auch scheint der «Weg» zum Chaos von sogenannten Phasenverdopplungen begleitet zu sein. Und selbst im chaotischen Bereich gibt es wieder schöne Muster (siehe meine Abbildung oben).

Der Phasenraum ist eine einfache Darstellung, um chaotische Systeme zu untersuchen. Bildet die Trajektorie im Phasenraum eine geschlossene Kurve, verhält sich das System nicht chaotisch und erlaubt eine Vorhersage. Umgekehrt ist eine offene Trajektorie ein starker Hinweis auf ein chaotisches Verhalten.