Inhaltsverzeichnis
Beschreibung einer Schwingung
Lernziele
- Sie kennen die physikalischen Grössen, die für die Beschreibung einer Schwingung nötig sind und verwenden Sie korrekt
- Sie berechnen korrekt die Position eines harmonisch schwingenden Körpers anhand der Bewegungsgleichung
Begriffe
Für die Beschreibung einer Schwingung braucht es sowohl eine räumliche als auch eine zeitliche Information.
Räumliche Information
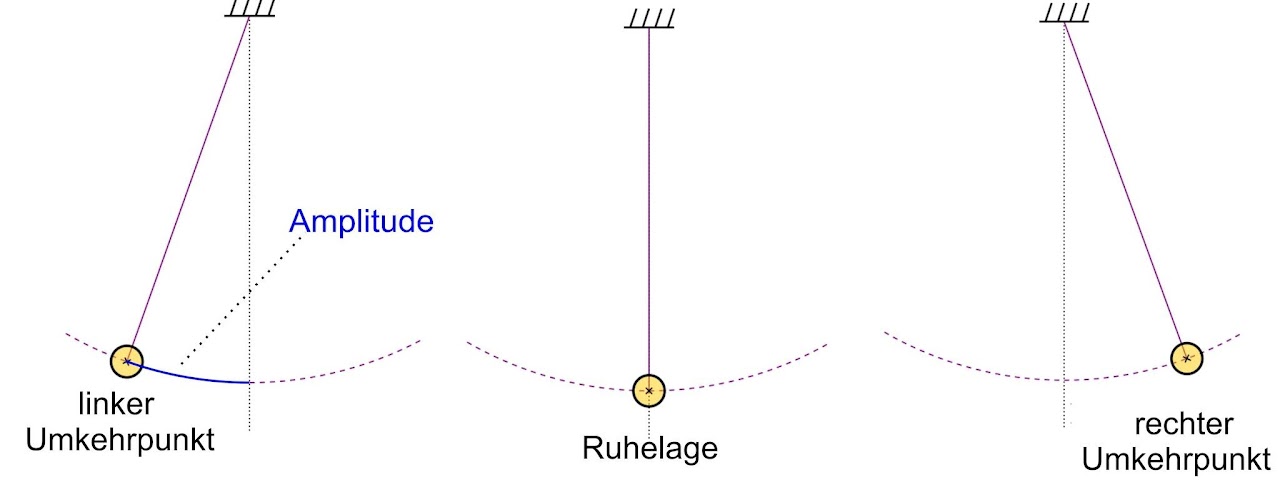
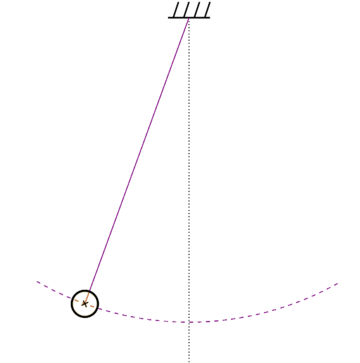Mit der Amplitude $\hat{y}$ bezeichnet man die maximale Auslenkung, die ein schwingender Körper gemessen zur Ruheposition einnimmt. Dort befindet sich das Pendel in den sog. Umkehrpunkten, ändert also seine Bewegungsrichtung.
Die momentane Auslenkung eines Pendels wird Elongation $y$ genannt.
Beide Grössen werden in der Einheit Meter (m) angegeben.
Zeitliche Information
Da eine Schwingung eine sich wiederholende Bewegung ausführt, lassen sich wie bei der Kreisbewegung 2 zeitliche Grössen angeben:
- Die Schwingungsdauer $T$ gibt die Zeitspanne für eine volle Schwingung an. Das ist die Zeitspanne, die das Fadenpendel beispielsweise braucht, um vom linken Umkehrpunkt wieder in den linken Umkehrpunkt zu gelangen. NB: Um vom linken in den rechten Umkehrpunkt zu gelangen, wird die halbe Schwingungsdauer benötigt. Die Schwingungsdauer wird in Sekunden (s) angegeben.
- Mit der Frequenz $f$ wird die Anzahl vollen Schwingungen angegeben, die ein Pendel in einer vorgegebenen Zeitspanne ausführt. Die Einheit der Frequenz ist Hertz (Hz).
Es gilt der von der Kreisbewegung bekannte Zusammenhang:
$$f=\frac{1}{T}$$
Aufgabe
Überlegen Sie sich, wo die räumlichen Informationen beim Federpendel gefunden werden. Fertigen Sie dazu eine Skizze an und tragen Sie die Amplitude $\hat{y}$ und eine beliebige Elongation $y$ des Federpendels ein.
Beschreibung einer harmonischen Schwingung
Nun sollen die Bewegungsgleichungen einer harmonischen Schwingung hergeleitet werden. Glücklicherweise lassen sie sich auf eine gleichförmige Kreisbewegung zurückführen. Schauen Sie sich dazu den Film der ETHZ an. Dort wird gezeigt, dass die Bewegung eines Fadenpendels mit derjenigen einer Kreisbewegung zusammenfällt, wenn beide von der Seite betrachtet werden.
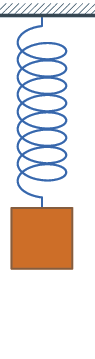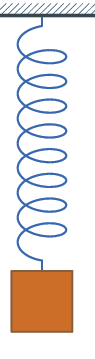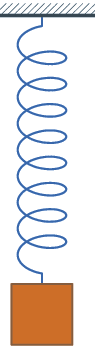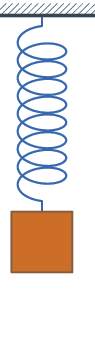
Dasselbe gilt auch für ein Federpendel. Dort wird die Kreisbewegung vertikal und nicht horizontal ausgeführt. Sie finden dieses Experiment auf folgendem Arbeitsblatt:
Arbeitsblatt zur Beschreibung einer harmonischen Schwingung
Aufgaben
Lösen Sie das Arbeitsblatt. Falls Sie irgendwo nicht weiter kommen, schauen Sie sich die Hilfen an:
Hilfe für die zeitliche Abhängigkeit des Winkels
Lösen Sie anschliessend Aufgabe 4 auf Seite 135. Die Diagramme bei d) dürfen Sie selbstverständlich mit einem entsprechenden Programm zeichnen (GeoGebra, Desmos, CAS-Rechner etc.)